【機器學習2021】自注意力機制 (Self-attention) (上)
Summary
TLDR本次讲解介绍了自注意力机制(Self-Attention)的概念和应用。自注意力机制能够处理输入序列中向量数量变化的问题,如文本处理、语音信号和社交网络等。通过计算序列中各个向量的相关性,自注意力机制能够捕捉到序列内部的复杂关系,从而生成考虑了整个序列信息的新向量。这种方法不仅提升了模型对序列数据的理解,也为后续的全连接网络提供了更丰富的输入。
Takeaways
- 🔍 自我注意力(Self-Attention)是一种网络架构,用于处理输入序列中各元素之间的关系。
- 🌟 自我注意力机制可以解决传统神经网络无法有效处理可变长度输入序列的问题。
- 📈 输入序列中的每个元素都可以通过自我注意力机制与序列中的其他元素进行关联性评分。
- 🤔 自我注意力机制通过Query(查询向量)、Key(关键向量)和Value(值向量)三者之间的关系来计算注意力分数。
- 📊 通过点积(Dot Product)计算Query和Key之间的关联性,得到初始的注意力分数。
- 🧠 利用Soft-Max函数对注意力分数进行归一化,得到每个元素的重要性权重。
- 🔄 通过加权求和的方式,结合Value向量和对应的注意力分数,生成新的输出向量。
- 🔢 自我注意力机制可以应用于文本处理、语音信号处理、社交网络分析等多种场景。
- 📚 词嵌入(Word Embedding)是一种表示词汇的方法,能够捕捉到词与词之间的语义关系。
- 🎧 语音信号处理中,通过将声音切割成帧(Frame)并转换成向量,可以应用自我注意力机制进行分析。
- 🌐 自我注意力机制是Transformer网络架构的核心组件,后者在自然语言处理等领域取得了显著的成果。
Q & A
Self-Attention是解决什么问题的?
-Self-Attention旨在解决当神经网络的输入是一个序列,且序列长度不一致时的问题。它允许模型处理不同长度的输入序列,并且能够捕捉序列内部元素之间的关系。
在Self-Attention中,输入序列的每个元素是如何表示的?
-在Self-Attention中,输入序列的每个元素都会被表示为一个向量,这些向量组成了一个向量集合。例如,在文本处理中,每个词汇都会被转换成一个词向量。
One-Hot Encoding在表示词汇时有什么缺点?
-One-Hot Encoding的缺点在于它假设所有的词汇之间都是没有关系的。通过这种方式表示的向量中没有任何语义信息,无法表达词汇之间的相似性或关联性。
Word Embedding是如何克服One-Hot Encoding的缺陷的?
-Word Embedding通过给每个词汇提供一个富有语义信息的向量来克服One-Hot Encoding的缺陷。在Word Embedding中,相似或相关的词汇在向量空间中会彼此接近,从而保留了语义关系。
在语音信号处理中,如何将一段声音信号表示为向量序列?
-在语音信号处理中,通过选取一段固定长度的声音信号(称为Window),将Window内的信号转换成一个向量(称为Frame)。然后,通过将Window逐步向右移动(通常移动10毫秒),来连续提取整个声音信号的向量序列。
Self-Attention模块是如何计算两个向量之间的关联性的?
-Self-Attention模块通过计算两个向量的点积(Dot-Product)来确定它们之间的关联性。具体方法是将输入向量与两个不同的权重矩阵相乘,得到两个新向量,然后将这两个新向量进行点积运算,得到的结果即为关联性分数α。
Self-Attention中的Query、Key和Value分别代表什么?
-在Self-Attention中,Query代表查询向量,用于搜索序列中与自己相关的其他向量;Key代表关键向量,与Query进行关联性计算;Value代表值向量,是序列中实际的元素。通过计算Query与所有Key的关联性分数,然后用这些分数对Value进行加权求和,得到最终的输出向量。
为什么在Self-Attention中要使用Soft-Max函数?
-Soft-Max函数在Self-Attention中用于将关联性分数转换为一个概率分布,这样每个Query向量都能得到一个关于序列中其他向量的注意力分布。Soft-Max通过指数化并归一化分数,确保所有关联性分数的和为1,从而可以作为权重来使用。
Self-Attention模块的输出是如何生成的?
-Self-Attention模块的输出是通过计算每个Query向量与所有Key向量的关联性分数,并使用这些分数对相应的Value向量进行加权求和来生成的。这样,每个输出向量都能综合考虑整个输入序列的信息。
Self-Attention机制可以如何应用在不同的任务中?
-Self-Attention机制可以应用于各种需要处理序列数据的任务中,例如文本处理中的词性标注、情感分析,语音信号处理中的声音识别,以及社交网络分析等。通过让模型关注序列中不同部分的重要性,Self-Attention能够提高模型处理序列数据的能力。
Self-Attention模块可以叠加使用吗?
-是的,Self-Attention模块可以叠加使用。在实际应用中,可以将Self-Attention模块的输出再次输入到另一个Self-Attention模块中,以便更深入地捕捉序列内部的复杂关系。这种叠加使用的方式可以增强模型对序列数据的理解。
Self-Attention模块在Transformer架构中扮演什么角色?
-在Transformer架构中,Self-Attention模块是核心组件之一。它负责处理输入序列,并生成能够反映序列内部关系的输出向量。Transformer架构通过Self-Attention模块实现了对序列数据的高效处理,从而在很多自然语言处理任务中取得了显著的成果。
Outlines
🌟 自我注意力机制的引入
本段落介绍了自我注意力(Self-Attention)机制的基本概念和目的。自我注意力机制旨在解决神经网络处理输入序列时的问题,特别是当序列长度不一致时。例如,在文本处理中,每个句子的长度不同,传统的神经网络难以处理这种变长的输入。自我注意力机制通过赋予序列中每个元素不同的权重,使得网络能够关注到与当前元素最相关的其他元素,从而更好地处理序列数据。
📝 序列标注问题与应用场景
这一部分讨论了序列标注问题,即输入和输出的序列长度相同的情况,并举了几个应用实例,如词性标注、语音识别和社交网络分析。这些应用中,每个输入元素都需要一个对应的标签或分类。此外,还提到了三种可能的输出类型:每个向量对应一个标签、整个序列对应一个标签、以及机器需要自己决定输出标签的数量。
🚧 全连接网络的局限性
在这一段中,指出了全连接网络在处理序列数据时的局限性。尤其是当序列中的元素需要根据上下文进行不同的处理时,全连接网络无法有效区分相同输入但应产生不同输出的情况。为了解决这个问题,提出了使用上下文信息的方法,即将序列中的多个向量一起输入到网络中,让网络能够考虑到更广泛的上下文信息。
🔄 自我注意力机制的工作原理
本段落详细解释了自我注意力机制的工作原理。自我注意力机制能够接收整个序列的输入,并输出考虑了整个序列信息的向量。通过使用查询(Query)、键(Key)和值(Value)的概念,自我注意力机制能够计算序列中每个元素与其他元素的相关性,并根据这些相关性对序列中的信息进行加权汇总,从而得到新的序列表示。
🧠 计算注意力分数和权重
这一部分深入讲解了如何计算注意力分数和权重。首先,通过查询和键的点积来计算每个元素之间的关联程度,得到注意力分数。然后,使用Soft-Max函数对分数进行归一化,得到每个元素的权重。最后,根据这些权重,将序列中的值向量加权求和,得到最终的输出向量。这个过程允许模型集中关注与当前任务最相关的序列部分。
Mindmap
Keywords
💡自注意力(Self-Attention)
💡网络架构
💡向量
💡Word Embedding
💡序列
💡分类(Classification)
💡回归(Regression)
💡标签(Label)
💡序列到序列(sequence to sequence)
💡Transformer
Highlights
介绍了Self-Attention网络架构,它是处理输入序列长度不一致问题的关键技术。
Self-Attention可以处理输入序列中每个元素与其他元素之间的关系,而不仅仅是局部窗口内的上下文信息。
Self-Attention通过计算序列中每个向量与其他所有向量的相关性,来捕捉全局依赖关系。
Self-Attention机制允许模型对序列中的每个元素赋予不同的权重,这些权重反映了元素间的重要性。
介绍了One-Hot Encoding和Word Embedding两种将词汇表示为向量的方法,并讨论了它们的优缺点。
Word Embedding能够捕捉词汇间的语义关系,如动物和植物的聚集,而One-Hot Encoding则无法表示这种关系。
通过声音信号处理的例子,解释了如何将一段声音信号转换为一系列向量,并用于模型的输入。
讨论了Graph结构在机器学习中的应用,如社交网络和分子结构,以及如何将这些结构表示为向量序列。
解释了三种不同的输出类型:每个向量对应一个标签、整个序列对应一个标签、以及序列到序列的任务。
提出了序列标注(Sequence Labeling)的概念,即给序列中的每个元素分配一个标签。
讨论了Fully-Connected Network在处理序列数据时的局限性,特别是在处理词性标注等任务时。
通过Self-Attention机制,模型能够考虑整个输入序列的信息,而不仅仅是局部窗口。
介绍了Self-Attention的计算过程,包括Query、Key和Value的概念以及它们在计算注意力分数中的作用。
解释了如何通过Soft-Max函数对注意力分数进行归一化,以便在序列中分配权重。
讨论了Self-Attention可以多次叠加使用,以进一步捕捉序列中的复杂关系。
提到了Transformer架构,这是Self-Attention机制的代表性应用,由Google提出。
强调了Self-Attention在处理自然语言处理和其他序列数据任务中的重要性和实用性。
讨论了Self-Attention在不同领域的潜在应用,如情感分析、语音识别和药物发现。
解释了Self-Attention如何通过权重和来提取序列中的关键信息,并生成新的向量表示。
Transcripts
好 接下來要講什麼呢
講完了CNN以後
我們要講另外一個常見的Network架構
這個架構叫做Self-Attention
而這個Self-Attention
想要解決的問題是什麼呢
它想要解決的問題是
到目前為止啊
我們的Network的Input都是一個向量
不管是在預測這個
YouTube觀看人數的問題上啊
還是影像處理上啊
我們的輸入都可以看作是一個向量
然後我們的輸出
可能是一個數值
這個是Regression
可能是一個類別
這是Classification
但假設我們遇到更復雜的問題呢
假設我們說
輸入是一排向量呢
而且這個輸入的向量的數目
是會改變的呢
我們剛才在講影像辨識的時候
我還特別跟你強調說
我們假設輸入的影像大小
都是一樣的
那現在假設我們的輸入
會不一樣呢
每次我們Model輸入的Sequence的數目
Sequence的長度都不一樣呢
那這個時候應該要怎麼處理
好 那有什麼樣的例子是
輸入是一個Sequence
而且長度會改變的呢
第一個例子
是文字處理
假設我們今天要Network的輸入
是一個句子的話
每一個句子的長度都不一樣嘛
每個句子裡面詞彙的數目都不一樣嘛
如果我們把一個句子裡面的每一個詞彙
都描述成一個向量
用成向量來表示的話
那我們的Model的輸入
就會是一個Vector Set
而且這個Vector Set的大小
每次都不一樣
句子的長度不一樣
那你的Vector Set的大小就不一樣
那有同學可能會問說
那怎麼把一個詞彙表示成一個向量呢
那簡單來說 最簡單的做法
是One-Hot的Encoding
你就開一個很長很長的向量
這個向量的長度啊
跟世界上存在的詞彙的數目是一樣多的
假設英文是十萬個詞彙
你就開一個十萬維的向量
每一個維度對應到一個詞彙
Apple就是100
Bag就是010
Cat就是001
以此類推
但是這樣子的表示方法有一個非常嚴重的問題
什麼樣嚴重的問題呢
它假設所有的詞彙彼此之間
都是沒有關係的
從這個向量裡面你看不到說
也許Cat跟Dog都是動物
所以他們比較接近
Cat跟Apple
一個動物一個植物
所以他們比較不相像
看不出來這件事情
這個向量裡面
沒有任何語義的資訊
有另外一個方法叫做Word Embedding
Word Embedding就是
我們會給每一個詞彙一個向量
而這個向量是有語義的資訊的
如果你把Word Embedding畫出來的話
你會發現
所有的動物可能聚集成一團
所有的植物可能聚集成一團
所有的動詞可能聚集成一團等等
那Word Embedding是怎麼得到的呢
這個就不是今天講課的重點了
如果你有興趣的話
可以看一下以下的錄影
總之你現在在網路上
可以載到一種東西叫做Word Embedding
這個Word Embedding
會給每一個詞彙一個向量
而一個句子就是一排長度不一的向量
好 那接下來還有什麼樣的例子
我們需要把
這個一個向量的Sequence當做輸入呢
舉例來說 作業二
一段聲音訊號其實是一排向量
怎麼說呢
我們會把一段聲音訊號取一個範圍
這個範圍 叫做一個Window
把這個Window裡面的資訊呢
描述成一個向量
這個向量就叫做一個Frame
在語音上
我們會把一個向量叫做一個Frame
通常這個Window的長度啊
就是25個Millisecond
那怎麼把這麼一個小段的聲音訊號
變成一個Frame
變成一個向量呢
這邊就有百百種做法啦
那這邊就不細講
就是有各式各樣的做法
可以用一個向量來描述
一小段25個Millisecond裡面的語音訊號
然後呢
你為了要描述一整段的聲音訊號
你會把這個Window往右移一點
通常移動的大小是10個Millisecond
欸 有人就會問說
為什麼這邊是25 為什麼這個10
這個問題呢 就很難回答
這個古聖先賢幫你調好了
你知道嗎
這個你自己調放都是比較差
這古聖先賢已經把所有的可能都試過了
然後調一個最好的結果
然後就這樣
好 那總之呢
一段聲音訊號
你就是用一串向量來表示
而因為每一個Window啊
他們往右移 都是移動10個Millisecond
所以一秒鐘的聲音訊號有幾個向量呢
有100個
所以一分鐘的聲音訊號
就有這個100乘以60
就有6000個向量
所以語音其實很複雜的
一小段的聲音訊號
它裡面包含的資訊量其實是非常可觀的
所以聲音訊號也是一堆向量
還有什麼東西是一堆向量呢
一個Graph
一個Graph 一個圖
也是一堆向量
怎麼說呢
我們知道說Social Network就是一個Graph
在Social Network上面每一個節點
就是一個人
然後節點跟節點之間的Each
就是他們兩個
比如說是不是朋友等等
而每一個節點
可以看作是一個向量
你可以拿每一個人的
比如說他的Profile裡面的資訊啊
他的性別啊 他的年齡啊
他的工作啊 他講過的話啊等等
把這些資訊用一個向量來表示
所以一個Social Network 一個Graph
你也可以看做是一堆的向量所組成的
那還有什麼例子跟Graph有關呢
舉例來說
一個分子
它也可以看作是一個Graph
那現在像這種Drug Discovery的應用
非常地受到重視
尤其是在Covid-19這一段時間
很多人都期待
也許用機器學習
可以在Drug Discovery上面做到什麼突破
那這個時候
你就需要把一個分子
當做是你的模型的輸入
每一個分子可以看作是一個Graph
分子上面的每一個球
就是一個原子
你就是一個向量
那一個原子怎麼用一個向量來表示呢
你可以用One-Hot Vector來表示
你可以說氫就是1000
碳就是0100
然後這個氧就是0010
你可以用One-Hot Vector
來表示每一個原子
那一個分子就是一個Graph
它就是一堆向量
好 那輸出是什麼
我們剛才已經看說輸入是一堆向量
它可以是文字
可以是語音
可以是Graph
那這個時候
我們有可能有什麼樣的輸出呢
有三種可能性
第一種可能性是
每一個向量都有一個對應的Label
也就是說當你的模型
看到輸入是四個向量的時候
它就要輸出四個Label
而每一個Label
它可能是一個數值
那就是Regression的問題
如果每個Label是一個Class
那就是一個Classification的問題
但是在第一種可能性裡面
輸入跟輸出的長度是一樣的
所以模型不需要去煩惱
要輸出多少的Label
輸出多少的Scale(00:07:29)
反正輸入是四個向量
輸出就是四個向量
輸入五個向量
輸入五個向量 輸出就是五個Label
這是第一種類型
那什麼樣的Applications
會用到第一種類型的輸出呢
舉例來說 在文字處理上
假設你今天要做的是POS Tagging
POS Tagging是什麼呢
POS Tagging就是詞性標註
你要讓機器自動決定說
每一個詞彙 它是什麼樣的詞性
它是名詞 還是動詞 還是形容詞等等
那這個任務啊
其實並沒有很容易
舉例來說
你現在看到一個句子
I saw a saw
這並不是打錯
並不是你看一個看
而是我看到一個鋸子
這個第二個saw當名詞用的時候
它是鋸子
不是Sentence那個句子
是可以鋸東西的鋸子
知道嗎
好 那所以機器要知道說
第一個saw是個動詞
第二個saw 雖然它也是個saw
但它是名詞
但是每一個輸入的詞彙
都要有一個對應的輸出的詞性
這個任務就是
輸入跟輸出的長度是一樣的Case
這個就是屬於第一個類型的輸出
那如果是語音的話
你可以想想看我們作業二
就是這樣子的任務
雖然我們作業二
沒有給大家一個完整的Sequence
我們是把
每一個每一個每一個Vector分開給大家了啦
但是串起來就是一段聲音訊號裡面
有一串Vector
每一個Vector你都要決定
它是哪一個Phonetic
也就是哪一個
我也不知道Phonetic是什麼
就是當做音標來看
就是哪一個音標
當然這個不是真正的語音辨識啦
這是一個語音辨識的簡化版
或者是如果是Social Network的話
就是給一個Graph
給一個Social Network
那你的Machine呢
你的Model呢
要決定每一個節點
它有什麼樣的特性
比如說他會不會買某一個商品
這樣我們才知道說
要不要推薦某一個商品給他
好 所以以下
以上呢
就是舉輸入跟輸出 數目一樣的例子
好 這是第一種可能的輸出
第二種可能的輸出是什麼
第二種可能的輸出是我們一整個Sequence
只需要輸出一個Label就好
舉例來說
如果是文字的話
我們就說Sentiment Analysis
Sentiment Analysis是什麼呢
Sentiment Analysis就是給機器看一段話
它要決定說這段話呢
是正面的還是負面的
那你可以想像說這種應用很有用
假設你的公司開發了一個產品
這個產品上線了
你想要知道網友的評價怎麼樣
但是你又不可能一則一則網友的留言都去分析
那也許你就可以用這種
Sentiment Analysis的技術
讓機器自動去判讀說
當一則貼文裡面有提到某個產品的時候
它是正面的 還是負面的
那你就可以知道你的產品
在網友心中的評價怎麼樣
這個是Sentiment Analysis給一整個句子
只需要一個Label
那Positive或Negative
那這個就是第二類的輸出
那如果是語音的例子的話呢
在作業四裡面我們會做語者辨認
機器要聽一段聲音
然後決定他是誰講的
這個也是第二種輸出的例子
或者是如果是Graph的話呢
今天你可能想要給一個分子
然後要預測說這個分子
比如說它有沒有毒性
或者是它的親水性如何
那這就是給一個Graph 輸出一個Label
這也是第二個例子
好 那還有第三個可能的輸出
第三個可能的輸出就是
我們不知道應該輸出多少個Label
機器要自己決定
應該要輸出多少個Label
可能你輸入是N個向量
輸出可能是N'個Label
為什麼是N'
機器自己決定
好 那這種任務啊
又叫做sequence to sequence的任務
那我們在作業五呢
會有sequence to sequence的作業
所以這個之後我們還會再講
那可以想像說
翻譯就是sequence to sequence的任務
因為輸入輸出是不同的語言
它們的詞彙的數目本來就不會一樣多
或者是語音辨識也是
真正的語音辨識也是一個sequence to sequence的任務
輸入一句話
然後輸出一段文字
這也是一個sequence to sequence的任務
好 那第三種類型之後會講
今天我們只講第一種類型
第二種類型
我們有作業四
你可以把作
你可以自己去看看作業四的程式
看看第一種類型的問題是怎麼處理的
那因為上課時間有限
所以上課
我們今天就先只講第一個類型
也就是輸入跟輸出數目一樣多的狀況
那這種輸入跟輸出數目一樣多的狀況啊
它又叫做Sequence Labeling
你要給Sequence裡面的每一個向量
都給它一個Label
那要怎麼解Sequence Labeling的問題呢
那直覺的想法就是
欸 就跟作業二一樣
我們就拿個Fully-Connected的Network
然後雖然這個輸入是一個Sequence
但我們就各個擊破
不要管它
不要管它是不是一個Sequence
各個擊破
把每一個向量
分別輸入到Fully-Connected的Network裡面
然後呢
Fully-Connected的Network就會給我們輸出
那現在看看
你要做的是Regression還是Classification
產生正確的對應的輸出
就結束了
那這麼做顯然有非常大的瑕疵
什麼樣非常大的瑕疵呢
假設今天是
詞性標記的問題
你給機器一個句子
I saw a saw
對Fully-Connected Network來說
這一個saw 跟這個saw
完全一模一樣啊
它們是同一個詞彙啊
既然Fully-Connected的Network輸入同一個詞彙
它沒有理由輸出不同的東西啊
但實際上
你期待第一個saw要輸出動詞
第二個saw要輸出名詞
但對Network來說它不可能做到
因為這兩個saw 明明是一模一樣的
你叫它這個要輸出動詞 要輸
這個要輸出名詞
它會非常地困惑
完全不知道要怎麼處理
所以怎麼辦
有沒有可能讓Fully-Connected的Network
考慮更多的
比如說上下文的Context的資訊呢
這是有可能的
怎麼做
你就把這一個向量
前後幾個向量都串起來
一起丟到Fully-Connected的Network就結束了
事實上在作業二裡面
助教也已經這麼做了
在作業二裡面
我們不是只看一個Frame
去判斷這個Frame屬於哪一個Phonetic
也就屬於哪一個音標
而是看這個Frame的前面五個加後面五個
也就總共看十一個Frame
來決定它是哪一個音標
所以我們可以給Fully-Connected的Network
一整個Window的資訊
讓它可以考慮一些上下文的
跟我現在要考慮的這個向量
相鄰的其他向量的資訊
但是這樣子的方法還是有極限
如果是在作業二
其實用這個方法就夠好了
作業二就算是給你Sequence的資訊
你考慮整個Sequence
你可能也很難再做的更好啦
作業二考慮前後五個Frame
其實就可以得到很不錯的結果了
所以你要過Strong Baseline
重點並不在於考慮整個Sequence
你就不需要往那個方向想了
用助教現有給你的Data
你就可以輕易的過Strong Baseline
好 但是真正的問題
但是如果今天我們有某一個任務
不是考慮一個Window就可以解決的
而是要考慮一整個Sequence才能夠解決的話
那要怎麼辦呢
那有人可能會想說這個還不容易
我就把Window開大一點啊
大到可以把整個Sequence蓋住
不就結束了嗎
但是不要忘了今天Sequence的長度
是有長有短的
我們剛才有說
我們輸入給我們的Model的Sequence的長度
每次可能都不一樣
如果你今天說我真的要開一個Window
把整個Sequence蓋住
那你可能要統計一下你的訓練資料
然後看看你的訓練資料裡面
最長的Sequence有多長
然後開一個Window比最長的Sequence還要長
你才有可能把整個Sequence蓋住
但是你開一個這麼大的Window
意味著說你的Fully-Connected的Network
它需要非常多的參數
那可能不只運算量很大
可能還容易Overfitting
所以有沒有更好的方法
來考慮整個Input Sequence的資訊呢
這就要用到我們接下來要跟大家介紹的
Self-Attention這個技術
那Self-Attention是怎麼運作的呢
Self-Attention的運作方式就是
Self-Attention會吃一整個Sequence的資訊
然後你Input幾個Vector
它就輸出幾個Vector
比如說你這邊Input一個深藍色的Vector
這邊就給你一個另外一個Vector
這邊給個淺藍色
它就給你另外一個Vector
這邊輸入4個Vector
它就Output 4個Vector
那這4個Vector有什麼特別的地方呢
這4個Vector
他們都是考慮一整個Sequence以後才得到的
那等一下我會講說Self-Attention
怎麼考慮一整個Sequence的資訊
所以這邊每一個向量
我們特別給它一個黑色的框框
代表說它不是一個普通的向量
它是考慮了整個句子以後才得到的資訊
再把這個有考慮整個句子的向量
丟進Fully-Connected的Network
然後再來決定說它應該是什麼樣的東西
什麼樣的類別或Output什麼樣的數字
那你用這個方法
如此一來你這個Fully-Connected的Network
它就不是只考慮一個非常小的範圍
或一個小的Window
而是考慮整個Sequence的資訊
再來決定現在應該要輸出什麼樣的結果
那這個就是Self-Attention
那Self-Attention呢不是只能用一次
你可以疊加很多次
你可以說
我這個Self-Attention的輸出呢
通過Fully-Connected Network以後
得到Fully-Connected Network的輸出
Fully-Connected的Network輸出
再做一次Self-Attention
Fully-Connected的Network
再過一次Self-Attention
再重新考慮一次整個Input Sequence的資訊
再丟到另外一個Fully-Connected的Network
最後再得到最終的結果
所以你可以把Fully-Connected的Network
跟Self-Attention交替使用
就是Self-Attention處理整個Sequence的資訊
Fully-Connected的Network
專注於處理某一個位置的資訊
然後你可以再用Self-Attention
再把整個Sequence資訊再處理一次
然後交替使用Self-Attention跟Fully-Connected
那有關Self-Attention
最知名的相關的文章
就是Attention is all you need.
那在這篇Paper裡面呢
Google提出了Transformer這樣的Network架構
那Transformer就是變形金剛
所以提到這個Network的時候呢
我們就會有變形金剛這個形象
那在Transformer裡面一個最重要的Module
Transformer我們今天還不會講到
但我們之後會講到
Transformer裡面一個最重要的Module呢
就是Self-Attention
它就是變形金剛的火種源
那這篇Paper最厲害的地方
就是它有一個霸氣的名字
它霸氣的名字就是Attention is all you need.
那其實像Self-Attention這樣的架構
最早我並不會說它是出現在
Attention is all you need.這樣的Paper
因為其實很多更早的Paper
就有提出過類似的架構
只是不見得叫做Self-Attention
比如說叫做(00:19:02)Self-Matching
或者是叫別的名字
不過呢是Attention is all you need.這篇Paper
把Self-Attention這個Module
把它發揚光大
那Self-Attention是怎麼運作的呢
Self-Attention的Input
它就是一串的Vector
那這個Vector可能是你整個Network的Input
它也可能是某個Hidden Layer的Output
所以我們這邊不是用x來表示它
我們用a來表示它
代表說它有可能是前面已經做過一些處理
它是某個Hidden Layer的Output
那Input一排a這個向量以後
Self-Attention要Output另外一排b這個向量
那這個b呢 每一個b呢
都是考慮了所有的a以後才生成出來的
所以這邊刻意畫了非常非常多的箭頭
告訴你說b1 考慮了a1到a4產生的
b2考慮a1到a4產生的
b3 b4也是一樣
考慮整個input的sequence
才產生出來的
好 那接下來呢就是要跟大家說明
怎麼產生b1這個向量
那你知道怎麼產生b1這個向量以後
你就知道怎麼產生剩下b1 b2 b3 b4剩下的向量
好 怎麼產生b1這個向量呢
第一個步驟
是根據a1找出這個sequence裡面
跟a1相關的其他向量
我們知道說今天我們要做self-attention
目的就是為了要考慮整個sequence
但是我們又不希望把整個sequence
所有的資訊包在一個window裡面
所以我們有一個特別的機制
這個機制是根據a1這個向量
找出說整個很長的sequence裡面
到底哪些部分是重要的
哪些部分跟判斷a1是哪一個label
是有關係的
哪些部分是我們要決定a1的class
決定a1的regression數值的時候
所需要用到的資訊
好 那每一個向量跟a1的關聯的程度
我們用一個數值叫α來表示
再來的問題就是這個self-attention的module
怎麼自動決定兩個向量之間的關聯性呢
你給它兩個向量a1跟a4
它怎麼決定a1跟a4有多相關
然後給它一個數值α呢
那這邊呢你就需要一個計算attention的模組
這個計算attention的模組呢
它就是拿兩個向量作為輸入
然後它就直接輸出α那個數值
那你就可以把α那個數值
當做兩個向量的關聯的程度
那怎麼計算這個α的數值呢
這邊就有各種不同的做法
那比較常見的做法呢
叫做用dot product
那dot product怎麼做呢
你把輸入的這兩個向量
分別乘上兩個不同的矩陣
左邊這個向量乘上Wq這個矩陣
右邊這個向量乘上Wk這個矩陣
接下來得到q跟k這兩個向量
那你再把q跟k做dot product
就是把他們做element-wise 的相乘
再全部加起來以後就得到
就把q跟k做dot product以後
得到一個 scalar
這個scalar就是α
這是一種計算α的方式
那其實還有其他的計算方式
比如說右邊呢
有另外一個叫做Additive的計算方式
它的計算方法就是
把同樣這兩個向量通過Wq Wk
得到q跟k
那我們不是把它做Dot-Product
是把它這個串起來
然後丟到這個過一個(00:22:39)Funtion
然後再通過一個Transform
然後得到α
總之有非常多不同的方法
可以計算Attention
可以計算這個α的數值
可以計算這個關聯的程度
但是在接下來的討論裡面
我們都只用左邊這個方法
這也是今日最常用的方法
也是用在Transformer裡面的方法
那接下來呀我們就要講
怎麼計算出這個α
那講完這個
這邊我們就快要講到一個段落
那講到一個段落呢
我們就可以下課或者看看大家有沒有問題
總之呢我們就是用這兩個Vector
可以計算出α
那接下來怎麼把它套用在Self-Attention裡面呢
那你就要把這邊的a1去跟這邊的a2 a3 a4
分別都去計算他們之間的關聯性
也就是計算他們之間的α
那怎麼做呢
你把a1乘上Wq 得到q1
那這個q有一個名字
我們叫做Query
它就像是你搜尋引擎的時候
去搜尋相關文章的問題
就像搜尋相關文章的關鍵字
所以這邊叫做Query
然後接下來呢
a2 a3 a4你都要去把它乘上Wk
得到k這個Vector
k這個Vector呢有一個名字叫做Key
那你把這個Query q1
跟這個Key k2
算Inner-Product就得到α
我們這邊用α1,2來代表說
Query是1提供的
Key是2提供的時候
這個1跟2他們之間的關聯性
這個我們用α1,2來表示
那這個α這個關聯性也有一個稱號
叫做Attention的Score
叫做Attention的分數
好那q1跟k2
也就是a1跟a2
計算出他們的Attention的分數
計算出他們的關聯性以後
接下來也要跟a3 a4來計算
那怎麼跟a3 a4計算呢
你就把a3乘上Wk 得到k3
得到另外一個Key
a4乘上Wk 得到k4
得到另外一個Key
然後你再把k3這個Key
跟q1這個Query做Inner-Product
得到1跟3之間的關聯性
得到1跟3的Attention
你把k4跟q1做Dot-Product
得到α1,4
得到1跟4之間的關聯性
你就把a1去計算它跟a2 a3 a4的關聯性
這個關聯性用的Attention Score α來表示它
那其實一般在實作時候
q1也會跟自己算關聯性
所以你也會把a1乘上Wk 得到k1
把q1跟k1去計算它的關聯性
自己跟自己計算的關聯性
那自己跟自己計算關聯性這件事情有多重要呢
你可以自己在做作業的時候試試看
看這件事情的影響大不大了
好 那我們計算出
a1跟每一個向量的關聯性以後
接下來這邊會作為一個Soft-Max
裡面有點有 這邊這個Soft-Max
跟分類的時候的那個Soft-Max是一模一樣的
我們就把這邊的α全部乘上Exponential
然後再把Exponential的值
全部加起來做Normalize
得到α'
所以Soft-Max的輸出就是一排α
所以本來有一排α
通過Soft-Max就得到α'
那你可能會問說這邊為什麼要用Soft-Max
剛才你說這個分類用Soft-Max
你說有一串道理 只是沒有講而已
那這邊有道理嗎
這邊就沒有什麼道理
這邊你不一定要用Soft-Max
你可以用別的東西 也沒問題
比如說有人嘗試過說做個ReLU
這邊通通做個ReLU
那結果發現還比Soft-Max好一點
所以這邊你不一定要用Soft-Max
這邊你要用什麼Activation Function都行
你高興就好
你可以試試看
那Soft-Max是最常見的
那你可以自己試試看
看能不能試出比Soft-Max更好的結果
好 那得到這個α'以後
接下來得到這個α'以後
接下來我們就要根據這個α'
去抽取出這個Sequence裡面重要的資訊
根據這個α我們已經知道說
哪些向量跟a1是最有關係的
接下來我們要根據這個關聯性
根據這個Attention的分數
來抽取重要的資訊
怎麼抽取重要的資訊呢
我們會把a1到a4這邊每一個向量
乘上Wv 得到新的向量
那這邊分別就是用v1 v2 v3 v4來表示
接下來把這邊的v1到v4
每一個向量都去乘上Attention的分數
都去乘上α'
然後呢再把它加起來
我們把式子寫在這邊
我們就是把這邊的每一個v都乘上α'
得到b1
那你可以想見說
如果某一個向量它得到的分數越高
比如說如果a1跟a2的關聯性很強
這個α'得到的值很大
那我們今天在做Weighted Sum以後
得到的b1的值
就可能會比較接近v2
所以這邊誰的值最大
誰的那個Attention的分數最大
誰的那個v就會Dominant你抽出來的結果
好 所以這邊呢我們就講了
怎麼從一整個Sequence 得到b1
4.7 / 5 (32 votes)


【人工智能】万字通俗讲解大语言模型内部运行原理 | LLM | 词向量 | Transformer | 注意力机制 | 前馈网络 | 反向传播 | 心智理论
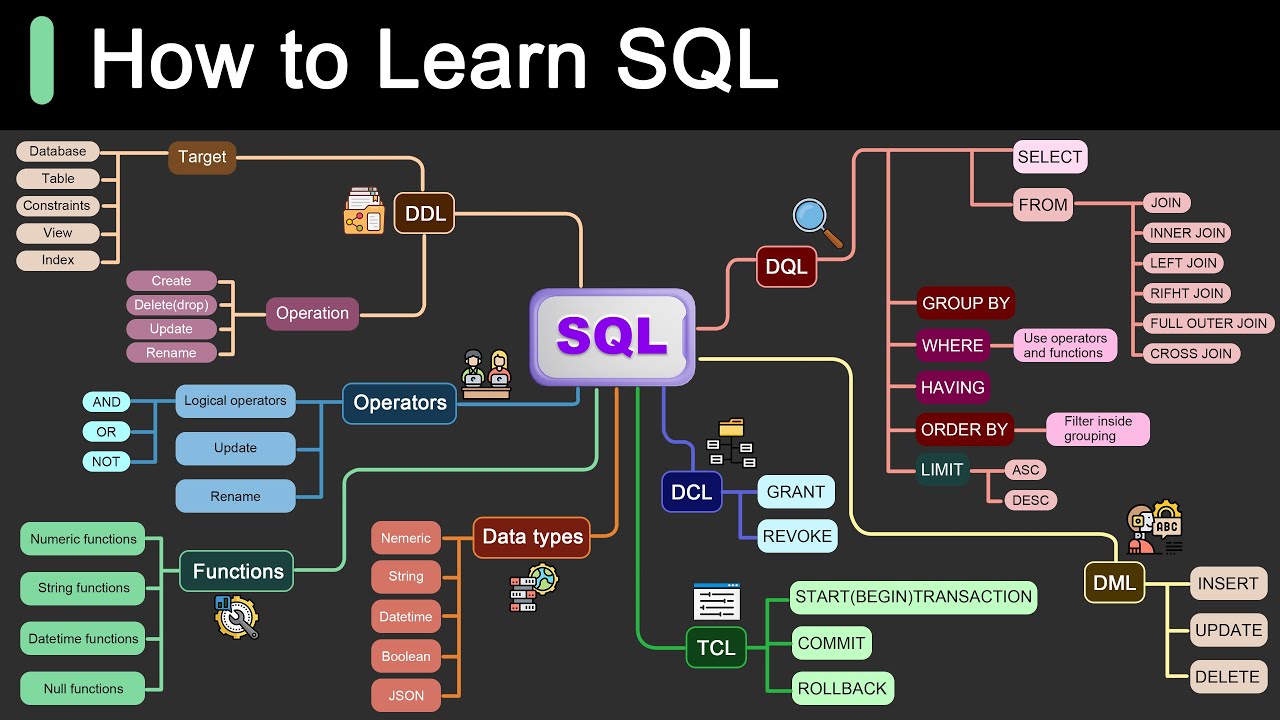
Roadmap for Learning SQL

Microsoft's New PHI-3 AI Turns Your iPhone Into an AI Superpower! (Game Changer!)

Risk-Based Alerting (RBA) for Splunk Enterprise Security Explained—Bite-Size Webinar Series (Part 3)

Simple Introduction to Large Language Models (LLMs)

How to accelerate in Splunk